Design of the R8000 Microprocessor

MIPS Technologies, Inc.

2011 N. Shoreline Blvd.

P.O. Box 7311

Mountain View, CA 94039-7311


June 2, 1994

Introduction

The magnitude of the task becomes clear when one considers that in 1991 the most advanced microprocessor achieved only tens of megaflops. We decided we could realistically get one order of magnitude performance improvement by a combination of silicon technology and processor organization, and another order of magnitude from multiprocessing. Accordingly the multiprocessor configuration was assumed from the beginning and a lot of design optimizations were made with this in mind.

Supercomputers and microprocessors evolved from a very different ancestry. Supercomputers are descendents of "general purpose data processors" with a history of numeric computing on large data sets. Microprocessors, on the other hand, descended from controllers that ran small programs in confined environments. Traditionally, microprocessors perform very well on smaller integer applications such as word processors and spreadsheets. They do not perform well when confronted with large data sets typical of the supercomputing environment.

Although supercomputers are usually characterized by their impressive floating-point compute speeds, in reality it is their memory size and bandwidth that differentiate them from other computers.To be useful, a multiply-add pair requires between one and three memory accesses to go with it. A several hundred megaflop microprocessor therefore will need a memory hierarchy that can deliver gigabytes per second of bandwidth. This kind of bandwidth is very easily provided from a little on-chip cache of, say, 16-Kbyte. However, one cannot compute for very long in a 16-Kbyte cache before exhausting all the data in it, at which time the processor must wait while the cache is refilled.

The obvious solution to attaining high bandwidth is to send loads and stores through a pipelined memory system. Unfortunately this is not desirable because accessing main memory takes a long time causing loads to have a very high latency, and such high-bandwidth memory systems are very expensive. It is well known that increasing load latencies directly impacts the execution speed of integer programs such as operating systems and compilers as well as the scalar portion of floating-point programs. These programs prefer to execute from a small, fast on-chip cache which is backed up by a large second-level cache off chip.

We designed a rather unusual "split level cache" to solve these conflicting requirements. Integer and address data resides in a small, fast on-chip cache. Floating-point data bypasses the on-chip cache and resides in a very large (up to 16-Mbyte) external cache that is somewhat slower. This external cache also acts as a second-level cache for the on-chip instruction and integer/address data cache. Hardware maintains coherence between the on-chip data cache and the external cache so there are no programming difficulties.

The split level cache scheme achieves good performance and ease of use for both supercomputer applications as well as standard workstation applications. Parallel floating-point compute-intensive applications use the multi-megabyte external cache as a "local memory" to hold blocked matrices (the external cache is set associative to make this easier). The operating system and traditional integer applications use the two level cache hierarchy in the conventional way. Coherence is maintained within each processor and across multiple processors. Programmers see a simple, flat shared virtual memory. (R8000 supports 64-bit addresses and integers.)

We envisioned R8000 microprocessors in high-end workstations and compute servers operating in a networked environment with other workstations and database servers. Binary compatibility across all platforms is essential to make such an environment friendly and productive. Most applications would be administered and stored on a single node and made available through the network. It is highly desirable for the same binary to operate on all platforms.

The binary compatibility requirement was one of the driving forces that lead us to a superscalar implementation. Vector architectures are known to work well for many floating-point applications: they are relatively simple to design, and compilers have had a long history of transforming vector loops. The disadvantages of vector architectures are that they do not scale to low-cost designs (e.g. $5000 workstations) and that the vector hardware is almost useless for general purpose integer applications. Furthermore, adding vector facilities to the MIPS instruction set would have caused a very large and traumatic change that seriously jeopardizes binary compatibility across our product line. For these reasons we reject the vector architecture approach.

Superscalar techniques provide comparable performance as vector techniques by issuing and executing multiple scalar instructions in parallel each cycle. A multiple-issue superscalar implementation of the MIPS instruction set can achieve high floating-point performance while still retaining binary compatibility with existing single-issue implementations used in lower-end workstations. With the advent of submicron silicon technology and very large dies, we felt that the logic complexity inherent in superscalar designs was a good trade-off to gain binary compatibility.

We chose to issue and complete instructions in-order in the integer pipeline because we believed that the design verification effort to validate an out-of-order pipeline would take longer and require more people than the design effort itself, a luxury we did not have. The floating-point pipeline is decoupled from the integer pipeline and supports out-of-order execution of floating-point instructions with respect to integer instructions, but the floating-point instructions themselves are issued in-order with respect to each other. Exceptions detected in the integer pipeline, such as illegal opcodes and invalid memory addresses, are precisely trapped. Exceptions detected in the floating-point pipeline, such as divide-by-zero, are normally trapped imprecisely, but for compatibility the processor supports a Precise Exception mode at degraded performance.

The initial product frequency of the R8000 chipset is 75MHz. At this frequency R8000 can issue four instructions per cycle to achieve 300 mips. Two of the four instructions per cycle can be double-precision fused multiply-add operations for a total of 300 mflops. R8000 supports two double-precision loads or stores per cycle for a cache throughput of 1.2 gigabytes per second.

This paper presents the R8000 microprocessor organization. We have attempted to highlight the more interesting features and discuss the thinking behind these design decisions. The paper begins with an overview of the processor chip set and pipeline structure. Then we discuss one of the more difficult problems in superscalar design: how to predict branches and dispatch instructions quickly enough to keep the execution units busy. After that we turn to the split level cache: interleaving for high bandwidth, hiding the latency of off-chip accesses and maintaining coherence between on-chip and off-chip caches. The paper concludes with some chip facts and performance comparisons.

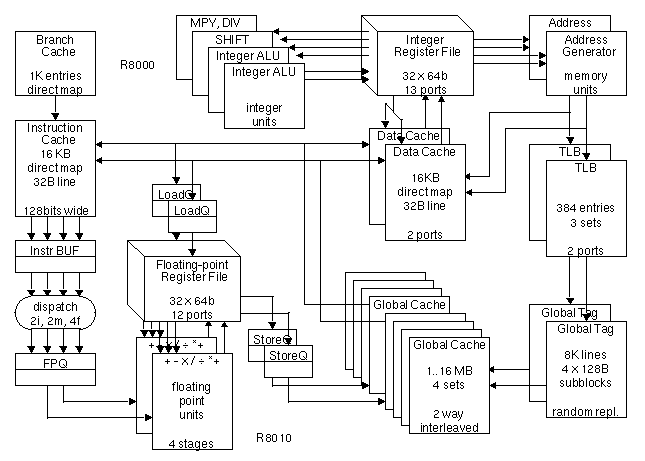
Figure 1-1: Block diagram of the R8000 microprocessor.

Processor Overview

Instructions are fetched from an on-chip 16-Kbytes instruction cache (Instruction Cache). This cache is direct mapped with a line size of 32 bytes. Four instructions (128 bits) are fetched per cycle. The instruction cache is virtually indexed and virtually tagged, and is refilled from the external cache in 11 cycles. There is a branch prediction cache (Branch Cache) associated with the instruction cache. The branch cache is also direct mapped and contains 1K entries. Details of the branch cache will be discussed later.

We chose a virtually tagged instruction cache for several reasons. A physically tagged instruction cache requires that there be an associated instruction translation lookaside buffer (ITLB), which introduces a performance penalty when it misses. A virtually tagged instruction cache avoids both the logic complexity of the ITLB as well as the performance penalty of ITLB misses. Further, a virtually tagged instruction cache can improve performance by allowing the contents to not be a subset of the external second-level cache, thus avoiding displacement by data accesses that sweep the second-level cache. The complexity of physically tagged caches is usually justified on the grounds that it is easier to maintain coherence in a multiprocessing system. However, the MIPS architecture requires operating system intervention when writing into the instruction stream, so it is possible for system software to maintain coherence in instruction caches. We chose a virtually tagged instruction cache to eliminate as much complexity as possible from the instruction fetch path, which is a very critical path in the machine.

Instructions from the cache are buffered (Instr BUF) and realigned before going to the dispatch logic. Up to four instructions chosen from two integer, two memory, and four floating-point instruction types may be dispatched per cycle. Floating-point instructions are dispatched into a queue (FPQ) where they can wait for resource contention and data dependencies to clear without holding up the integer dispatching. In particular, the FPQ decouples the floating-point unit to hide the latency of the external cache. This will be discussed in more detail later.

Integer and memory instructions get their operands from a 13 port register file (Integer Register File). Integer function units consist of two integer ALUs, one shifter, and one multiply-divide unit. The ALUs and shifter operate in one cycle. The multiply-divide unit is not pipelined. The latency for 32 bit or 64 bit multiply is 4 or 6 cycles, respectively. The latency for division varies from 21 to 73 cycles depending on the number of significant digits in the result. Up to two integer operations may be initiated every cycle.

Memory instructions, which have register+offset or register+register address modes, go through the address generation units (Address Generator) and then to the translation lookaside buffer (TLB). The TLB is a three way set associative cache containing 384 entries. It is dual-ported so that two independent memory instructions can be supported per cycle. TLB misses are serviced by a software handler which uses random replacement. Integer loads and stores go to the on-chip data cache (Data Cache). It, too, is dual-ported to support two loads or one load and one store per cycle. The Data Cache is 16-Kbytes direct-mapped with a line size of 32 bytes. It is virtually addressed and physically tagged. The Data Cache is a proper subset of the external cache and hardware maintains coherence.

The Instruction Cache and Data Cache miss penalty has a very strong impact on performance, especially on integer codes which gets all of its data from the Data Cache. Both the Instruction Cache and the Data Cache refill from the external cache, which delivers 16 bytes at a time. The Data Cache refill time is 7 cycles: five to go through the external cache rams (described later) and two cycles to write the 32 byte line. The Instruction Cache refill time is longer (11 cycles) because it must be first be confirmed under branch prediction and then translated by the TLB before going to the external cache.

Floating-point loads and stores go directly off chip after translation to physical addresses and bypass the on-chip Data Cache. The external cache (Global Cache) is two-way interleaved to support two 64 bit loads or stores per cycle. It is configurable from one to 16-Mbytes in size. The external cache is four-way set associative, each cache line containing four sectors or subblocks each with its own state bits. The line size is configurable as 128, 256, or 512 bytes which corresponds to sector sizes of 32, 64, or 128 bytes, respectively. The external cache is implemented using a pair of custom tag rams (Global Tag) and from 8 to 36 commodity synchronous static rams depending on their width. The rams operate at the same frequency as the processor. Global Cache refill time depends on the system implementation.

The floating-point unit contains two execution datapaths each capable of double precision fused multiply-adds , simple multiplies, adds, divides, square-roots, and conversions. A twelve port register file (Floating-point Register File) feeds the execution datapaths, which are themselves fully bypassed. Short operations comprising compares and moves take one cycle. Medium operations comprising adds, multiples, and fused multiply-adds take four cycles and are fully pipelined. Long operations comprising divides and square-roots are not pipelined. Single and double precision divides take 14 and 20 cycles, respectively. The two datapaths are completely symmetric and indistinguishable to software--the compiler simply knows that it can schedule two floating-point operations per cycle. When one of the datapaths is busy with a non-pipelined operation, the other datapath can still execute one pipelined operation per cycle.

R8000 implements a superset of the MIPS R4000 64-bit instruction set. Future MIPS microprocessors will incorporate these instructions. There are three categories of new instructions: fused multiply-add, register+register addressing mode, and conditional moves. The fused multiply-add instructions have three input operands and performs a multiplication followed by an addition with no intermediate rounding. These instructions are available in both single and double precision. The register+register addressing mode is supported for floating-point loads and stores to enhance the performance of array accesses with arbitrary strides. A full complement of both integer and floating-point conditional moves that tests both integer and floating-point conditions were added, and the floating-point status register was extended to include a total of eight floating-point conditional code (cc) bits which can be individually set by comparison instructions. The compiler use conditional move (cmove) instructions to transform simple if-then-else constructs into straight-line code to reduce the frequency of branch misprediction. For example, the Fortran statement

if (A(i).gt.big) idx=i

fload %f2=A[%r1] -- i in %r1
cmp.gt %cc1=%f2>%f1 -- big in %f1
cmove 2=%r1?%cc1 -- idx in %r2

Integer Pipeline

Figure 1-2: Integer pipeline

This pipeline differs from the traditional RISC pipeline in two ways: there are actually four pipelines--two integer ALU pipelines and two load/store pipelines, and ALU operations occur in parallel with data cache accesses. The traditional RISC pipeline has a load shadow; the instruction cycle immediately after a load cannot use the result of the load. This was found acceptable for scalar pipelines because the compiler can frequently put some independent instruction after a load. However, the compiler would have to find four independent instructions to cover the same shadow in this superscalar pipeline, a rather unlikely scenario.

By delaying the ALU we remove the load shadow for load to ALU operations but create an ALU shadow for load addresses. There is an extra cycle of delay when an address calculated by an ALU instruction is used as the base address by the following load or store instruction. We found this trade-off to be advantageous because load-use dependencies occur more frequently than compute-load/store address dependencies, particularly in integer code with many branches which are not amenable to superscalar speedup. In addition, the new register+register addressing mode for floating-point loads and stores will help reduce the need for precalculated addresses. A disadvantage of putting the ALU further down the pipeline is that it adds an extra cycle to branch resolution. However, many conditional branches test the result of a load, and in the traditional RISC pipeline the extra cycle would have appeared as a load delay slot that may not be filled. We further mitigated branch penalties by using branch prediction to statistically hide the latency of branch resolution.

The integer pipeline includes a number of features to enhance parallel instruction execution. The MIPS instruction set defines all branches to have one delay slot after it. R8000 will execute the branch and its delay slot in parallel unless prevented by dependencies or lack of resources. The dual-ported Data Cache includes a bypass circuit so that the common case of a store followed by a possibly dependent load instruction can be executed in parallel. Hardware detects the matching addresses and enables the bypass at the byte level. Making the bypass handle all combinations of partial word stores and loads adds some logic to the datapaths but significantly simplifies the control logic--a good trade-off in this case.

Alignment-Free Instruction Dispatching

Conceptually what we need for alignment-free dispatching is a queue that can enqueue four aligned instructions and supports dequeueing 0, 1, 2, 3 or 4 instructions per cycle. Such a structure can be implemented in a straightforward manner as an 8-ported RAM but would be very expensive in area. We designed an instruction queue that takes advantage of the fact that the incoming instructions are naturally aligned on 128-bit boundaries and that the outgoing instructions are always contiguous, shown in Figure 1-3. Quadword aligned instructions are fetched from the cache and come in the top of the queue. The dispatch registers function as the traditional "instruction register" connected to decoders and register files. These registers can either be recirculated, filled from the on-deck registers, or filled from the output of the instruction buffers. The on-deck registers are essentially the last entry in the instruction buffer. Their purpose is to provide access to the last two entries of the buffer. The instruction buffer itself contains a bypass so that there is a direct path from the instruction cache to the dispatch registers.

Figure 1-4 illustrates the operation of the instruction queue. Assume that all the various registers and buffers are filled with instructions named by letters. In cycle 1 the dispatch logic determines that out of the first four potentially parallel instructions, only A and B can be executed

Figure 1-3: Instruction alignment and dispatch

simultaneously. (Perhaps instruction C is dependent on A, which would also preclude D since we preserve in-order dispatching.) Signals from the dispatch logic tells the multiplexors to move instructions E and F from the

Figure 1-4: Example of unaligned dispatching

on-deck registers to the dispatch registers while holding instructions C and D as shown in cycle 2. At this time the program counter points to C as the leading instruction, and priorities are assigned starting from there and wrapping around.

Cycle 3 illustrates how the fetch pipeline is decoupled from the dispatch decision logic. When instructions C, D and E are replaced by G, H and I, the on-deck registers are depleted. This event causes the buffer to advance filling all four on-deck registers and the instruction cache to fetch four new aligned instructions into the buffer. However, these actions occur in the next cycle so that the critical paths involving dispatch decisions need only manipulate the multiplexors feeding the dispatch registers. Cycle 4 shows the simultaneous advancement of the buffer and filling of dispatch registers to achieve continuous alignment-free instruction dispatching.

Predicting Branches

Figure 1-5: Branch prediction

instruction cache--thus eliminating almost all conflicts. Even so the branch prediction cache takes only about half the area of the instruction cache tags.

Figure 1-5 shows a block diagram of the instruction cache and branch prediction cache, a sample entry from the BCACHE, and an example of prediction. The Instruction Cache and the BCACHE are accessed in parallel in the Fetch stage of the pipeline. The output of the BCACHE contains a valid bit (v), the cache index of the branch target, the alignment of the last instruction in the source basic block (src), and the alignment of the target instruction (dst). The valid bit is set if there is a predicted discontinuity within this quadword, and it controls the multiplexor selecting whether the fetch program counter should be incremented by 4 instructions or loaded from the index field of the branch cache. At the same time, the src field forms a bitmask which invalidates instructions after the end of the basic block. The dst field is delayed one cycle and then is used to invalidate instructions at the target quadword but before the target instruction. Note that the delayed dst bitmask is or'ed with the new src bitmask so that a single quadword can have both invalidations on the left and also invalidations on the right, i.e. a very short basic block.

One reason the branch cache takes little area is because we only store the 10 bit cache index of the branch target as opposed to the full virtual address of the target. We get the remaining higher-order bits of the predicted target address from the tag of the target cache entry (recall that the instruction cache is virtually tagged) when we fetch it in the next cycle. This scheme implicitly assumes that all predicted branch targets hit in the cache. While this is frequently true it does increase the instruction cache miss penalty because miss detection cannot be confirmed until the Execute cycle when all predictions have been resolved. We did not explore the possibility of speculatively servicing an instruction cache miss even before it has been confirmed because doing so consumes valuable external cache bandwidth which we wanted to reserve for floating-point loads and stores.

The association of a single prediction for a quadword of instructions introduces the possibility of cache thrashing if there is more than one branch within the quadword. (The MIPS architecture defines all branches to include a delay slot which cannot be filled by another branch instruction. Therefore there can be at most two branches in a quadword of instructions.) We did not believe this was a big problem because (i) non-taken branches do not require a prediction, and (ii) compilers can be taught to avoid creating tiny basic blocks by using conditional move instructions to make the small amount of code unconditionally executable.

All branches are resolved in the Execute stage of the pipeline. Because the delay slot of branches may execute in the same cycle as the branch instruction or be delayed by some arbitrary amount due to dependencies, we actually associate the resolution of a branch with the delay slot of that branch reaching the Execute stage. At that time we check the program counter of the previous stage of the pipeline to determine whether the branch was correctly predicted (either taken or fall through). A mismatch between the correct program counter following the delay instruction and the program counter in the Address Generate stage of the pipeline indicates there has been a misprediction. Three penalty cycles are needed to repair a branch misprediction: the pipeline is flushed, the branch cache is updated, and fetching begins at the corrected program counter.

Our branch prediction scheme works uniformly for both the taken and fall-through cases, and in fact also works for jump register type instructions. Therefore we predict all types of branches and jumps including subroutine calls and returns with the same hardware. We originally chose this approach because it greatly simplified the pipeline control hardware, perhaps at the expense of some performance loss. Supprisingly we found this simple policy very effective for the emerging object-oriented programming paradigm using dynamic shared objects where it is common to call many small procedures indirectly via pointers. This programming style results in many jump register type instructions whose targets are actually invariant and thus are good candidates for branch prediction.

External Cache Organization

A key decision was what type of RAM to use. Very roughly, there is an order of magnitude difference in cost per bit between DRAMs and commodity SRAMs, and between commodity SRAMs and custom SRAMs embedded in logic chips. For example, in 1993 $250 buys 4-Mbytes of DRAM, 1-Mbytes of commodity SRAM, or a single custom chip containing 64 to 128-Kbytes of embedded SRAM. There are many advantages in using custom cache SRAMs: associativity with little speed penalty, streaming buffers that support restarting the CPU immediately after the critical word has arrived without waiting for the rest of the cache line, high-bandwidth writeback buffer that can evict an entire cache line from the RAM in a single cycle. The single disadvantage of custom cache SRAMs is cost--we estimated the external cache could only be 256 to 512-Kbytes if we used custom SRAMs.

In the end we chose to build a large external cache based on commodity SRAMs. The deciding factor was multiprocessor cost performance. In a uniprocessor, the higher miss rate of a smaller cache can be largely compensated by tightly coupling the memory system and exploiting burst-mode transfers from the DRAMs. In a multiprocessor, especially a bus-based multiprocessor, the majority of the delay to memory is consumed by bus arbitration and other overhead. The actual data transfer time is only a fraction of the total delay. Therefore streaming buffers and other overlapping techniques are much less effective in multiprocessors than in uniprocessors. A large, multi-megabyte cache is highly desirable in a bus-based multiprocessor because the miss rate is quite low for general applications, typically less than 1%, and also because well-tuned code (e.g. dividing matrices into blocks, each block being local to a single processor) can use the large cache as a local memory to minimize inter-processor communication. Compared to kilobyte-range caches, having multi-megabyte caches in a multiprocessor puts much less loading on the shared memory bus and allows more processors to be used effectively in a single system. This improves both the total performance as well as the cost effectiveness of the multiprocessor system by sharing main memory and the I/O subsystem across more processors.

Having decided on commodity SRAMs, we were faced with the problem of how to get enough bandwidth. We knew we wanted no less than a gigabyte/second of cache bandwidth. Using 12-15ns standard asynchronous SRAMs and taking into account address buffering and data skew, we could cycle the SRAMs in 20-25ns and thus would need four 64-bit wide banks of SRAMs to achieve this bandwidth. We rejected this solution as being too expensive and mechanically too unwieldy. Instead we decided to gamble on the Synchronous Static RAMs (SSRAM), which were in the process of becoming standardized in 1990-91. These RAMs integrate input and output registers onto the chip, thus pipelining the RAM access into three cycles: address setup, RAM access, and data output. This level of pipelining was sufficient to enable a large bank of SSRAMs to cycle at 10-12ns. Compared to conventional asynchronous static RAMs, SSRAMs can deliver roughly twice the bandwidth using the same basic silicon technology and I/O signals. We expected the cost premium of SSRAMs to be perhaps 20% higher than standard asynchronous SRAMs once they are produced in some quantity.

Using SSRAMs, we could deliver 1.2 gigabyte/second of bandwidth with just two 64-bit wide banks of cache. The entire cache including parity bits can be constructed with 16 or 36 RAM chips using by-9 or by-4 chips, respectively, in a very reasonable area.

Figure 1-6: Set associative tag ram

Another key question was associativity. Our previous experiences with multiprocessors indicated that associativity was highly desirable for second-level caches connected to shared memory busses. Very large direct mapped caches have the bad property that the same program may behave very differently when re-compiled (or even reallocated in physical memory) because minor changes in the positions of loops and subroutines can cause huge variations in the conflict miss rate. In bus-based multiprocessors this effect is exaggerated because the additional bus traffic slows down other processors.

The usual way to support associativity is to read multiple banks in parallel and then select data from the bank that hits. We rejected this approach since it required doubling or quadrupling the bandwidth from the cache chips. Another approach is to look up the sets serially, but we did not use this because we wanted to access the cache every cycle. Instead we chose to design a custom 4-way set associative tag ram as shown in Figure 1-6. The low-order bits of the physical address is used to index into both the tag ram and the data ram. The hit information is encoded into two bits and form the most-significant part of the address sent to the data SSRAM.This approach gives us associativity without increasing the number of SSRAMs. The downside is the additional latency of sequentially looking up the tag ram in series with accessing the data rams and, of course, the cost of the tag rams. We believed this was a good trade-off since the external cache is used for less latency-sensitive data. The tag rams are moderately dense custom static RAM chips: approximately 256-Kbit to support a 4-Mbytes cache, 1-Mbit to support a 16-Mbytes cache.

Figure 1-7 shows the external cache pipeline. Since there are two bands, addresses are sorted into odd and even doublewords within the R8000. There are five stages in the external cache pipeline. Addresses are sent from the R8000 to the tag ram in the first stage. The tags are looked up and hit/miss information is encoded in the second stage. The third stage is used for chip crossing from the tag ram to the data rams. The SSRAM is accessed internally within the chip in the forth stage. Finally data is sent back to the R8000 and R8010 in the fifth stage. We allocated a full cycle to chip crossing because TTL drivers with significant loading at 75 MHz require almost an entire cycle, and also because we wanted the chip-set to scale well to higher frequencies.

Figure 1-7: External cache pipeline

Resolving Conflicts in Interleaved Cache

The compiler can mitigate bank conflicts by careful code generation. For example, it knows that references to A[i] and A[i+1] will be to different banks of the cache. The problem arises when a subroutine with a loop references two different arrays A[] and B[] that are formal parameters. Because the compiler does not know what the base addresses of the arrays are, it cannot tell if references A[i] and B[i] will go to the same bank.

We designed hardware to help out the compiler by adding a one-deep queue called the "address bellow." Referring to Figure 1-7, the logic immediately following the integer pipeline consists of a crossbar for sorting even and odd references, and a register which forms the address bellow. Figure 1-8 illustrates the operation of the address bellow. Imagine a sequence of pairs of both even references and both odd references as shown. Without the address bellow the interleaved cache would only be able to process one half of a pair of references per cycle--the pipeline would be stalled every other cycle and so the machine would run at 50% efficiency. The purpose of the address bellow is to slightly reorder the reference pattern so as to improve the chances of even and odd references lining up in time. For example, the second even reference is enqueued in the address bellow and paired with the first odd reference from the next cycle, and so forth. We provided the address bellow to solve the local misalignment problem; the compiler is responsible for solving the global even/odd address mix problem. This has turned out to be a happy compromise between silicon area (and complexity) versus software complexity.

Figure 1-8: Effect of address bellow

Decoupling the Floating Point Unit

We chose to hide the external cache latency by decoupling the R8010 from the R8000 pipeline. Referring to Figure 1-7 , floating-point instructions are dispatched into a queue before going to the R8010. If a floating point load instruction is immediately followed by a compute instruction that uses the result of the load, the queue allows both instructions to be dispatched together as if the load had no latency at all. The integer pipeline is immediately free to continue on to other instructions. The load instruction proceeds down the external cache pipeline and deposits the load data in the load data queue after five cycles. In the mean time the compute instruction waits in the floating-point instruction queue until the load data is available.

By decoupling floating-point operations we achieve out of order execution of floating-point instructions with respect to integer instructions, thereby hiding the latency of the external cache. This limited form of out-of-order execution is an example of the 80/20 rule: we got most of the benefit of out-of-order execution while incurring only small amounts of extra complexity. In particular, by issuing instructions using first-in-first-out queues instead of a more general priority queue, we avoided a lot of verification efforts because the order of floating-point instruction execution is easily predictable. This is important because time needed for design verification quickly becomes a bottleneck in complex processors.

A consequence of decoupling the floating-point unit from the integer pipeline is that floating point exceptions become imprecise with respect to integer instructions. We briefly considered various schemes to achieve precise exceptions but quickly decided that they were too complicated to meet our development schedule. R8000 reports floating-point exceptions as an asynchronous interrupt some time after the event has occurred. Floating-point interrupts can be confined to arbitrary small regions of the program by periodically reading the floating-point status register, which has the side effect of flushing out all pending floating-point interrupts. For backward compatibility we provide a Precise Exception mode which stalls the integer pipeline whenever a floating-point instruction is being executed, thus making all the floating-point exceptions precise.

Coherence in Split Level Cache

One simplifying factor is that the external cache has very high write bandwidth, two 64-bit doublewords per cycle, for floating-point stores. We take advantage of this by making the on-chip integer data cache write-through. Complexity is minimized because there is no need for a write buffer between the on-chip cache and the external cache: the external cache can absorb write-through at full bandwidth. Making the on-chip cache write-through greatly simplifies multiprocessing support because we can invalidate lines from the on-chip cache at any time without worrying about write backs. However we did have to limit the on-chip cache to one store per cycle because there were not enough pins on the R8000 to write through more than one doubleword per cycle. Write-through traffic from the on-chip cache also blocks floating-point loads and stores, but we felt this performance penalty was acceptable because integer stores tend not to occur in highly-optimized loops that demand maximum floating-point load/store bandwidth.

The external cache uses a write-back policy to conserve bandwidth on multiprocessor busses. This means that the cache tags must be interrogated before stores are allowed to complete. This is implemented by two sets of address and data queues, one address and data pair for each bank of the cache. Stores are deferred in these queues while the cache tags are looked up and are released only if they hit in the cache.

One of the unique problems introduced by a split level cache is the coherence of integer and floating-point data. The problem is that while integer loads and stores access both the on-chip and external caches, floating-point loads and stores only access the external cache. For example, if a particular memory location is first written using an integer store, then rewritten using a floating-point store, a subsequent integer load would get stale data (from the integer store) unless something special was done.

The obvious solution is to invalidate the enclosing cache line from the on-chip cache whenever a floating-point store occurs. This preserves correctness but can lead to very poor performance. Consider the following example of C code:

struct { if (s.Ch[2]==...){
char Ch[4]; s.Flt =...
float Flt; 
int Ival; ...= s.Ival;
} s;

We solved this problem by attaching a valid bit to each 32-bit word within all on-chip cache lines. Integer stores of size 32 or 64 bits will set the corresponding valid bits, while floating-point stores will clear them. Integer stores smaller than 32 bits (e.g. bytes) require that the corresponding valid bit be on, otherwise it triggers a miss. Filling a line sets all the valid bits. Having finer granularity valid bits allow the above mentioned example cache line to both reside on chip and not contain floating-point data. This solution solves both the performance problem of mixed integer/float structures as well as the correctness problem of unions containing both integer and floating-point fields.

Conclusions

Acknowledgment

Related Literature

1. IBM RISC System/6000 Technology, IBM Corporation, 1990.

2. Norman Jouppi and David Wall, "Available Instruction-Level Parallelism for Superscalar and Superpipelined Machines", Third International Conference on Architectural Support for Programming Languages and Operating Systems, April, 1989, pp. 272-282.

3. Michael Smith, Mike Johnson, and Mark Horowitz, "Limits on Multiple Instruction Issue", Third International Conference on Architectural Support for Programming Languages and Operating Systems, April, 1989, pp. 290-302.

4. J. E. Smith, et. al., "The ZS-1 Central Processor", Second International Conference on Architectural Support for Programming Languages and Operating Systems, October, 1987, pp. 199-204

5. S. Przybylski, M. Horowitz, and J. Hennessy, "Characteristics of Performance-Optimal Multi-Level Cache Hierarchy", 16th Annual International Symposium on Computer Architecture, May, 1998, pp. 114-121.

6. IBM Journal of Research and Development, vol. 4, num. 1, January, 1990.

Hsu holds a BS degree in computer science from the University of Minnesota and MS and PhD degrees from the Univeristy of Illinois at Urbana. He is a member of IEEE.